某单位拟建一个扇环面形状的花坛(如图所示)，该扇环面是由以点
为圆心的两个同心圆弧和延长后通过点的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
米，圆心角为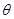
（弧度）．
（1）求
关于的函数关系式；
（2）已知在花坛的边缘(实线部分)进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为
，求关于
的函数关系式，并求出为何值时，取得最大值？
（本小题满分14分）一袋子中有大小、质量均相同的10个小球，其中标记“开”字的小球有5个，标记“心”字的小球有3个，标记“乐”字的小球有2个．从中任意摸出1个球确定标记后放回袋中，再从中任取1个球．不断重复以上操作，最多取3次，并规定若取出“乐”字球，则停止摸球．求：
（Ⅰ）恰好摸到2个“心”字球的概率；
（Ⅱ）摸球次数
的概率分布列和数学期望．
(本题满分14分) 在△ABC中, 角A, B, C所对的边分别为a, b, c, 且满足
.
(Ⅰ) 求
的值;
(Ⅱ) 若△ABC的面积是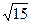
, 求
的值.
（本小题满分12分）
某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：
其中
是仪器的月产量.
（1）将利润表示为月产量的函数
；
（2）当月产量为何值时，公司所获得利润最大？最大利润是多少？
（本小题满分14分）
已知函数
且
，
（1）求
的值；
（2）判定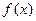
的奇偶性；
（3）判断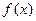在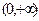
上的单调性，并给予证明．
（本小题满分12分）
（1）已知函数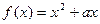
，且对任意的实数x都有
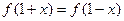成立，求实数a的值；
（2）已知定义在(－1，1)上的函数
是减函数，且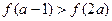
，求a的取值范围。