（本小题满分14分）如图，在四棱锥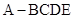
中，侧面
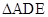为等边三角形，底面
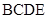是等腰梯形，且
，
，
，
，
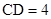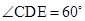为
的中点，
为
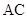的中点，且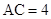
．
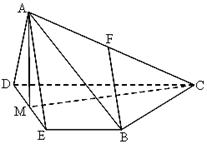
（1）求证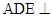：平面
平面
；
（2）求证：
平面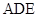
；
（3）求四棱锥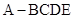的体积．
已知数列{bn}是首项为1，公差为2的等差数列，数列{an}的前n项和Sn=nbn．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设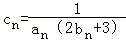
，求数列{cn}的前n项和Tn．
已知函数f（x）=（x+a）2+lnx．
（1）当a=
时，求函数f（x）在[1，+∞）上的最小值；
（2）若函数f（x）在[2，+∞）上递增，求实数a的取值范围；
（3）若函数f（x）有两个极值点x1、x2，且x1∈（0，
），证明：f（x1）﹣f（x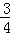2）＞
﹣ln2．
已知椭圆C：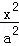
+
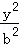=1（a＞b＞0）经过点（1，
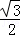），椭圆C的离心率e=
．
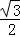（1）求椭圆C的方程；
（2）△ABC的三个顶点都在椭圆上，且△ABC的重心是原点O，证明：△ABC的面积是定值．
已知公比不为1的等比数列{an}的首项a1=
，前n项和为Sn，且a3+S5，a4+S4，a5+S3成等差数列．
（1）求等比数列{an}的通项公式；
（2）对n∈N+，在an与an+1之间插入3n个数，使这个3n+2个数成等差数列，记插入的这个3n个数的和为bn，且cn=
．求数列{cn}的前n项和Tn．
如图（1），在三角形ABC中，BA=BC=2
，∠ABC=90°，点O，M，N分别为线段的中点，将ABO和MNC分别沿BO，MN折起，使平面ABO与平面CMN都与底面OMNB垂直，如图（2）所示．
（1）求证：AB∥平面CMN；
（2）求平面ACN与平面CMN所成角的余弦；
（3）求点M到平面ACN的距离．