已知函数f（x）=（x+a）2+lnx．
（1）当a=
时，求函数f（x）在[1，+∞）上的最小值；
（2）若函数f（x）在[2，+∞）上递增，求实数a的取值范围；
（3）若函数f（x）有两个极值点x1、x2，且x1∈（0，
），证明：f（x1）﹣f（x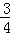2）＞
﹣ln2．
(本小题满分12分)已知二次函数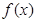
的二次项系数为
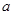，且不等式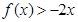
的解集为（1，3）。
（1）若方程
有两个相等的实数根，求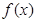的解析式；
（2）若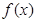的最大值为正数，求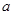的取值范围。
(本小题满分10分)已知等差数列{an}的首项a1＝1，公差d＞0，且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设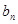
＝
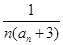（n∈N*），
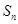＝b1＋b2＋…＋bn，是否存在最大的整数t，使得任意的n均有
总成立？若存在，求出t；若不存在，请说明理由
(本小题满分10分)已知A、B、C为△ABC的三内角，且其对边分别为a、b、c.若
, 
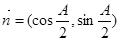，且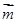
·
＝
.
（1） 求角A的大小； ⑵ 若a＝2
，三角形面积S＝，求b+c的值.
（本小题14分）已知四棱锥P-ABCD，底面ABCD是
、边长为
的菱形，又
，且PD=CD，点M、N分别是棱AD、PC的中点．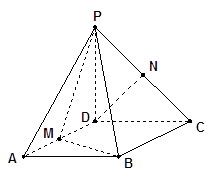
（1）证明：DN//平面PMB；
（2）证明：平面PMB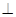
平面PAD；
（3）求点A到平面PMB的距离．
（本小题满分10分）如图，在三棱柱
—
中，点D是BC的中点，欲过点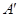
作一截面与平面
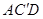平行，问应当怎样画线，并说明理由。