如图,平面 平面
平面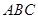 ,
,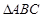 是等腰直角三角形,
是等腰直角三角形,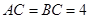 ,四边形
,四边形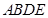 是直角梯形,
是直角梯形,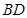 ∥AE,
∥AE,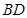

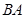 ,
, ,
,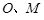 分别为
分别为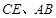 的中点.
的中点.
(1)求异面直线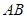 与
与 所成角的大小;
所成角的大小;
(2)求直线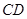 和平面
和平面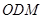 所成角的正弦值.
所成角的正弦值.
已知四棱锥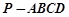 的底面是平行四边形,
的底面是平行四边形,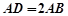 ,
,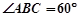 ,
,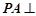 面
面 ,且
,且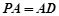 .若
.若 为
为 中点,
中点, 为线段
为线段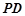 上的点,且
上的点,且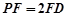 .
.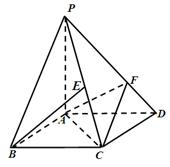
(1)求证: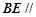 平面
平面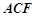 ;
;
(2)求PC与平面PAD所成角的正弦值.
已知数列 的前
的前 项和为
项和为 ,
, ,若
,若 成等比数列,且
成等比数列,且 时,
时, .
.
(1)求证:当 时,
时, 成等差数列;
成等差数列;
(2)求 的前n项和
的前n项和 .
.
已知函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
设函数 ,
, ,
, ,
,
(1)若曲线 与
与 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为 ,求
,求 的值;
的值;
(2)若 ,且
,且 ,
,
①求证: ; ②求证:
; ②求证: 在
在 上存在极值点.
上存在极值点.
如图,两条相交线段 、
、 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当 变化时,恒有
变化时,恒有 ?
?