已知数列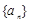 满足
满足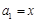 ,
,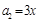 ,
,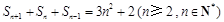 ,
,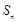 是数列
是数列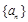 的前
的前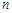 项和.
项和.
(1)若数列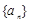 为等差数列.
为等差数列.
①求数列的通项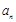 ;
;
②若数列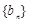 满足
满足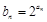 ,数列
,数列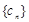 满足
满足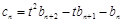 ,试比较数列
,试比较数列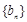 前
前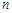 项和
项和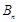 与
与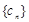 前
前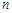 项和
项和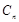 的大小;
的大小;
(2)若对任意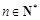 ,
,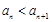 恒成立,求实数
恒成立,求实数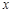 的取值范围.
的取值范围.
某学校篮球队、羽毛球队、乒乓球队的某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求: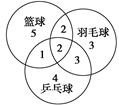
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为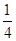 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是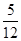 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是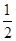 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?
已知圆 的参数方程为
的参数方程为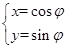 (
(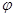 为参数),以坐标原点
为参数),以坐标原点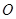 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.
(I)将圆 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(II)圆 、
、 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
分别求适合下列条件圆锥曲线的标准方程:
(1)焦点 为 、
、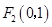 且过点
且过点
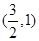 椭圆;
椭圆;
(2)与双曲线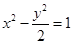 有相同的渐近线,且过点
有相同的渐近线,且过点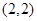 的双曲线.
的双曲线.
在面积为 的△ABC中,角A、B、C所对应的边为
的△ABC中,角A、B、C所对应的边为 成等差数列,
成等差数列,
B=30°.(1)求 ;(2)求
;(2)求 .
.