为了让学生了解更多“奥运会”知识，某中学举行了一次“奥运知识竞赛”，共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
|
0.16 |
| 70.5~80.5 |
10 |
|
| 80.5~90.5 |
18 |
0.36 |
| 90.5~100.5 |
|
|
| 合计 |
50 |
|
(1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…799， 试写出第二组第一位学生的编号；
(2)填充频率分布表的空格(将答案直接填在表格内) ，并作出频率分布直方图；
(3)若成绩在85.5~95.5分的学生为二等奖，问参赛学生中获得二等奖的约多少人？
（本题12分）现有甲、乙两个靶.某射手向甲靶射击一次，命中的概率为
，命中得
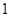分，没有命中得
分；向乙靶射击两次，每次命中的概率为
,每命中一次得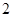
分，没有命中得分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.（1）求该射手恰好命中一次的概率；（2）求该射手的总得分
的分布列及数学期望
.
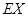（本题12分）某位收藏爱好者鉴定一件物品时，将正品错误地鉴定为赝品的概率为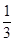
，将赝品错误地鉴定为正品的概率为
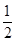，已知一批物品共有4件，其中正品3件，赝品1件.（1）求该收藏爱好者的鉴定结果为正品2件，赝品2件的概率；（2）求该收藏爱好者的鉴定结果中正品数
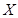的分布列及数学期望.
（本题12分）为了研究化肥对小麦产量的影响，某科学家将一片土地划分成200个
的小块，并在100个小块上施用新化肥，留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位：kg)
表1：施用新化肥小麦产量频数分布表
| 小麦产量 |
 |
 |
 |
 |
 |
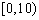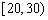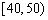| 频数 |
10 |
35 |
40 |
10 |
5 |
表2：不施用新化肥小麦产量频数分布表
| 小麦产量 |
|
|
|
|
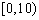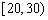| 频数 |
15 |
50 |
30 |
5 |
(10)完成下面频率分布直方图；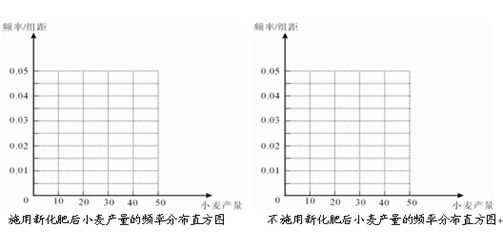
(2)统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量；
(3)完成下面2×2列联表，并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3：
| 小麦产量小于20kg |
小麦产量不小于20kg |
合计 |
|
| 施用新化肥 |
 |
 |
|
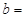| 不施用新化肥 |
 |
 |
|
| 合计 |
 |
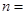附：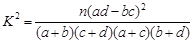
 |
0.050 |
0.010 |
0.005 |
0.001 |
 |
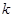3.841 |
6.635 |
7.879 |
10.828 |
（本题12分）某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据
| x |
6 |
8 |
10 |
12 |
| y |
2 |
3 |
5 |
6 |
（1）请画出上表数据的散点图；（2）请根据上表提供的数据，求出y关于x的线性回归方程
；（3）试根据（2）求出的线性回归方程，预测记忆力为9的同学的判断力.(相关公式：
，
)
（本题12分）已知在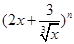
的展开式中，第
项的二项式系数与第2项的二项式系数的比为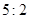
.（1）求
的值；（2）求含
的项的系数；（3）求展开式中系数最大的项．