一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
| |
轿车A |
轿车B |
轿车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
(1)求下表中z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数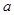 记这8辆轿车的得分的平均数为
记这8辆轿车的得分的平均数为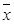 ,定义事件
,定义事件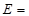 {
{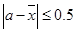 ,且函数
,且函数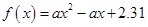 没有零点},求事件
没有零点},求事件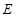 发生的概率
发生的概率
已知函数 在
在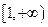 上为增函数,且
上为增函数,且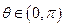 ,
,
(1)求 的值;
的值;
(2)若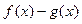 在
在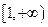 上为单调函数,求
上为单调函数,求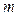 的取值范围;
的取值范围;
(3)设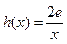 ,若在
,若在 上至少存在一个
上至少存在一个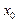 ,使得
,使得 成立,求
成立,求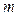 的取值范围。
的取值范围。
如图1,在直角梯形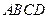 中,
中, 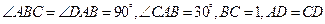 ,
,
把△ 沿对角线
沿对角线 折起后如图2所示(点
折起后如图2所示(点 记为点
记为点 ), 点
), 点 在平面
在平面 上的正投影
上的正投影 落在线段
落在线段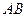 上,连接
上,连接 .
.
(1) 求直线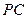 与平面
与平面 所成的角的大小;
所成的角的大小;
(2)求二面角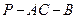 的大小的余弦值.
的大小的余弦值.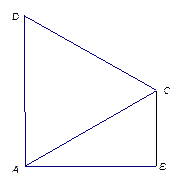
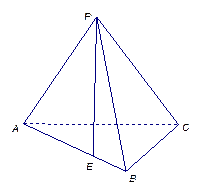
图1图2
解关于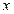 的不等式:
的不等式:
正定中学组织东西两校学生,利用周日时间去希望小学参加献爱
心活动,东西两校均至少有1名同学参加。已知东校区的每位同学往返车费是3元,
每人可为5名小学生服务;西校区的每位同学往返车费是5元,每人可为3位小学
生服务。如果要求西校区参加活动的同学比东校区的同学至少多1人,且两校区同
学去希望小学的往返总车费不超过37元。怎样安排东西两校参与活动同学的人数,
才能使受到服务的小学生最多?受到服务的小学生最多是多少?
本题满分12分)已知数列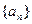 满足
满足 ,
,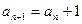 .
.
(1)求数列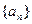 的通项公式;
的通项公式;
(2)设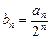 ,求数列
,求数列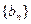 的前n项和Tn.
的前n项和Tn.