已知a,b,c分别为△ABC三个内角A,B,C的对边,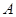 为
为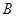 ,
,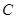 的等差中项.
的等差中项.
(1)求A;
(2)若a=2,△ABC的面积为 ,求b,c的值.
,求b,c的值.
给定椭圆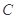 :
: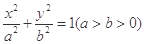 ,称圆心在原点
,称圆心在原点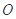 ,半径为
,半径为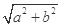 的圆是椭圆
的圆是椭圆 的“准圆”.若椭圆
的“准圆”.若椭圆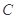 的一个焦点为
的一个焦点为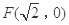 ,其短轴上的一个端点到
,其短轴上的一个端点到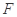 的距离为
的距离为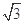 .
.
(1)求椭圆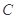 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点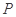 是椭圆
是椭圆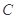 的“准圆”上的动点,过点
的“准圆”上的动点,过点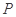 作椭圆的切线
作椭圆的切线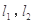 交“准圆”于点
交“准圆”于点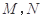 .
.
(ⅰ)当点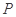 为“准圆”与
为“准圆”与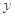 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线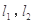 的方程并证明
的方程并证明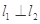 ;
;
(ⅱ)求证:线段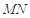 的长为定值.
的长为定值.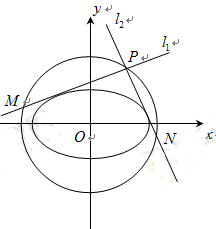
已知函数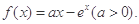
(1)若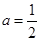 ,求函数
,求函数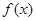 在
在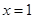 处的切线方程;
处的切线方程;
(2)当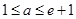 时,求证:
时,求证: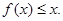
某公司销售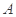 、
、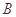 、
、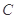 三款手机,每款手机都有经济型和豪华型两种型号,据统计
三款手机,每款手机都有经济型和豪华型两种型号,据统计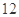 月份共销售
月份共销售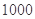 部手机(具体销售情况见下表)
部手机(具体销售情况见下表)
| A款手机 |
B款手机 |
C款手机 |
|
| 经济型 |
200 |
x |
y |
| 豪华型 |
150 |
160 |
z |
已知在销售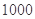 部手机中,经济型
部手机中,经济型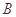 款手机销售的频率是
款手机销售的频率是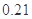 .
.
(1)现用分层抽样的方法在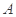 、
、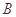 、
、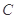 三款手机中抽取
三款手机中抽取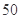 部,求在
部,求在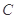 款手机中抽取多少部?
款手机中抽取多少部?
(2)若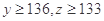 ,求
,求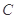 款手机中经济型比豪华型多的概率.
款手机中经济型比豪华型多的概率.
如图,四棱锥 中,
中,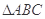 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
,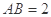 ,
, .
.
(1)若点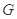 是
是 的中点,求证:
的中点,求证: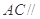 平面
平面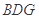
(2)若 是线段
是线段 的中点,求三棱锥
的中点,求三棱锥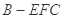 的体积.
的体积.
已知等差数列 满足
满足 ,
,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前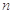 项和.
项和.