已知函数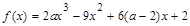 ,
,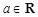 .
.
(1)若函数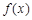 在
在 处取得极值,求实数
处取得极值,求实数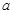 的值;
的值;
(2)若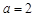 ,求函数
,求函数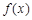 在区间
在区间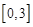 上的最大值和最小值.
上的最大值和最小值.
已知函数 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在原点处的切线方程;
在原点处的切线方程;
(Ⅱ)当 时,讨论函数
时,讨论函数 在区间
在区间 上的单调性;
上的单调性;
(Ⅲ)证明不等式 对任意
对任意 成立.
成立.
已知
 ,曲线
,曲线 上任意一点
上任意一点 分别与点
分别与点 、
、 连线的斜率的乘积为
连线的斜率的乘积为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设直线 与
与 轴、
轴、 轴分别交于
轴分别交于 、
、 两点,若曲线
两点,若曲线 与直线
与直线 没有公共点,求证:
没有公共点,求证: .
.
如图,已知多面体 的底面
的底面 是边长为
是边长为 的正方形,
的正方形, 底面
底面 ,
, ,且
,且 .
.
(Ⅰ)求多面体 的体积;
的体积;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
已知不等式2|x-3|+|x-4|<2a.
(Ⅰ)若a=1,求不等式的解集;
(Ⅱ)若已知不等式的解集不是空集,求a的取值范围.
已知曲线C1的极坐标方程为ρcos(θ- )=-1,曲线C2的极坐标方程为ρ=2
)=-1,曲线C2的极坐标方程为ρ=2 cos(θ-
cos(θ- ).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
).以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系.
(Ⅰ)求曲线C2的直角坐标方程;
(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.