如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求直线B1C1与平面A1BC1所成角的正弦值;
(2)在线段BC1上确定一点D,使得AD⊥A1B,并求 的值.
的值.
(本小题满分12分)如图,在四棱锥 中,
中,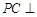 底面
底面 ,
, 是直角梯形,
是直角梯形, ,
,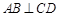 ,
, ,
, 是
是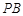 的中点.
的中点.
(1)求证;平面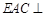 平面
平面 ;
;
(2)若二面角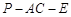 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面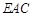 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)口袋中装有除颜色,编号不同外,其余完全相同的2个红球,4个黑球,现从中同时取出3个球.
(1)求恰有两个黑球的概率;
(2)记取出红球的个数为随机变量 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)设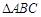 的内角
的内角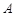 ,
,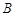 ,
, 所对的边分别为
所对的边分别为 ,
, ,
,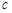 ,且
,且 .
.
(1)求角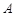 的大小;
的大小;
(2)若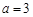 ,求
,求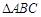 的周长
的周长 的取值范围.
的取值范围.
已知函数 .
.
(1)当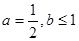 时,
时, 与
与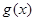 在定义域上单调性相反,求
在定义域上单调性相反,求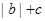 的最小值。
的最小值。
(2)当 时,求证:存在
时,求证:存在 ,使
,使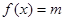 有三个不同的实数解
有三个不同的实数解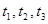 ,且对任意
,且对任意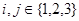 且
且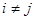 都有
都有 .
.
(本小题满分13分)已知抛物线C的顶点为O(0,0),焦点为F(0,1).
(1)求抛物线C的方程;
(2)过点F作直线交抛物线C于A,B两点.若直线AO,BO分别交直线l:y=x-2于M,N两点,求|MN|的最小值.