如图,在直三棱柱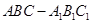 中,
中,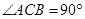 ,
,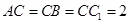 ,
,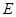 是
是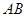 中点.
中点.
(1)求证: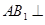 平面
平面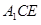 ;
;
(2)求直线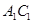 与平面
与平面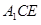 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)
在甲、乙等7个选手参加的一次演讲比赛中,采用抽签的方式随机确定每个选手的演出顺序(序号为1,2,……7),求:
(1)甲、乙两个选手的演出序号至少有一个为奇数的概率;
(2)甲、乙两选手之间的演讲选手个数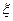 的分布列与期望.
的分布列与期望.
(本小题12分)
已知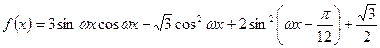 (其中
(其中 )的最小正周期为
)的最小正周期为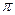 .
.
(1)求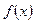 的单调递增区间;
的单调递增区间;
(2)在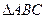 中,
中,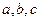 分别是角
分别是角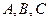 的对边,已知
的对边,已知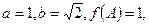 求角
求角 .
.
.(本小题满分14分)
已知数列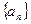 满足
满足 且
且
(1)求 ;
;
(2)数列 满足
满足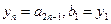 ,且
,且 时
时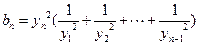 .
.
证明当 时,
时, 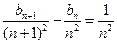 ;
;
(3)在(2)的条件下,试比较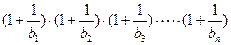 与4的大小关系.
与4的大小关系.
. (本小题满分13分)
设A ,B
,B 是椭圆
是椭圆 上的两点,
上的两点, 为坐标原点,向量
为坐标原点,向量 ,向量
,向量 。
。
(1)设 ,证明:点M在椭圆上;
,证明:点M在椭圆上;
(2)若点P、Q为椭圆上两点,且 ∥
∥ 试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
试问:线段PQ能否被直线OA平分?若能平分,请加以证明;若不能平分,请证明理由。
(本小题满分12分)
已知函数 .
.
(1)求a的取值范围;
(2)若对任意的 成立,求
成立,求 的取值范围。
的取值范围。