已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G、∠C=∠EFB=90°，∠E=∠ABC=30°，AB=DE=4．
（1）求证：△EGB是等腰三角形
（2）若纸片DEF不动，问△ABC绕点F逆时针旋转最小 度时，四边形ACDE成为以ED为底的梯形（如图（2））求此梯形的高．
（本小题满分8分）甲、乙两人准备整理一批新到的实验器材，若甲单独整理需
要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.
⑴问乙单独整理多少分钟完工？
⑵若乙因式作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？
（本小题满分8分）如图11，一转盘被等分成三个扇形，上面分别标有关－1，1，
2中的一个数，指针位置固定，转动转盘后任其自由停止，这时，鞭个扇形恰好停在指针所
指的位置，并相应得到这个扇形上的数（若指针恰好指在等分线上，当做指向右边的扇形）.
⑴若小静转动转盘一次，求得到负数的概率；
⑵小宇和小静分别转动一次，若两人得到的数相同，则称两人“不谋而合”，用列表法（或画树形图）求两人“不谋而合”的概率.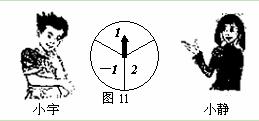
（本小题满分8分）如图10，在6×8的网格图中，每个小正方形边长均为1，点
O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1：2
⑵连接⑴中的AA′，求四边形AA′C′C的周长.（结果保留根号）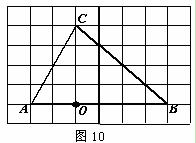
（本小题满分8分）
已知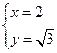
是关于x，y的二元一次方程
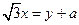的解.求(a＋1)(a－1)＋7的值
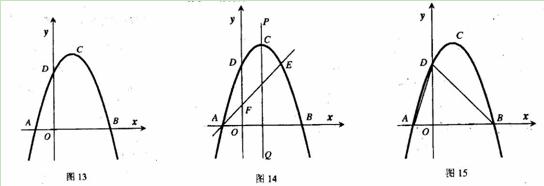
如图13，抛物线y=ax2＋bx＋c(a≠0)的顶点为（1,4），交x轴于A、B，交y轴于D，其中B点的坐标为（3,0）
（1）求抛物线的解析式
（2）如图14，过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，若直线PQ为抛物线的对称轴，点G为PQ上一动点，则x轴上是否存在一点H，使D、G、F、H四点围成的四边形周长最小.若存在，求出这个最小值及G、H的坐标；若不存在，请说明理由.
（3）如图15，抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD，若存在，求出点T的坐标；若不存在，说明理由.