如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.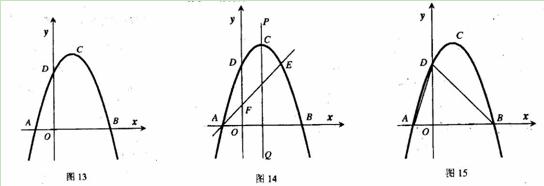
(11·钦州)
某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题: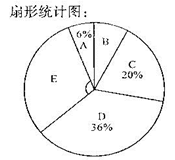 频数分布表扇形统计图
频数分布表扇形统计图
| 组别 |
成绩 |
频数 |
| A |
50≤x<60 |
3 |
| B |
60≤x<80 |
m |
| C |
70≤x<80 |
10 |
| D |
80≤x<90 |
n |
| E |
90≤x<100 |
15 |
(1)频数分布表中的m=_▲,n=_▲;
(2)样本中位数所在成绩的级别是_▲,扇形统计图中,E组所对应的扇形圆心角的度数是_▲;
(3)请你估计该校九年级的学生中,体育综合测试成绩不少于80分的大约有多少人?
(11·钦州)
如图,在平面直角坐标系中,点O为原点,反比例函数y=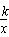 的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.
(11·钦州)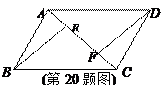 如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
如图,E、F是平行四边形ABCD对角线AC上的两点,BE∥DF.求证:BE=DF.
(11·钦州)先化简,再求值:(a+1)(a-1)+a (1-a),其中a=2012.
(11·柳州).
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C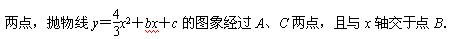

(1)求抛物线的函数表达式;
(2)设抛物线的顶点为D,求四边形ABDC的面积;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.