某市准备从7名报名者（其中男4人，女3人）中选3人到三个局任副局长.
（1）设所选3人中女副局长人数为X，求X的分布列和数学期望；
（2）若选派三个副局长依次到A、B、C三个局上任，求A局是男副局长的情况下，B局为女副局长的概率.
（用0，1，2，3，4，5这六个数字：
（1）能组成多少个无重复数字的四位偶数？
（2）能组成多少个无重复数字且比1325大
的四位数？
（．在一次购物抽奖活动中，假设某10张券中有一等奖奖券1张，可获价值50元的奖品；有二等奖奖券3张，每张可获价值10元的奖品；其余6张没奖。某顾客从此10张奖券中任抽2张，求：
（1）该顾客中奖的概率；
（2）该顾客获得的奖品总价值X（元）的概率分布列。
求以下问题的排列数：
（1）4男3女排成一排，3女相邻。
（2）4男3女排成一排
，女不能排在两端。
（3）4男3女排成一排，男女相间。(结果用数字表示)
甲、乙两人各进行3次射击，甲每次击中目标的概率为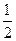
，乙每次击中目标的概率为
.
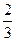（1）记甲击中目标的次数为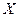
，求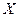的概率分布列及数学期望EX；
（2）求甲恰好比乙多击中目标2次的概率.
(14分) 已知函数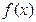
定义域为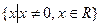
，对于定义域内的任意x,y都有
，且
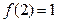，当