从某校高二年级 名男生中随机抽取
名男生中随机抽取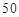 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成 组:第一组
组:第一组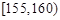 ,第二组
,第二组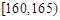 , ,第八组
, ,第八组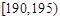 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
| 分组 |
频数 |
频率 |
频率/组距 |
| |
|
|
|
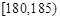 |
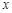 |
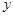 |
 |
 |
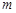 |
 |
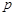 |
| |
|
|
|
频率分布直方图如下: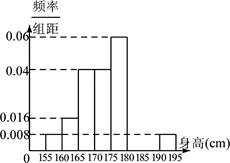
(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取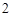 名男生,记他们的身高分别为
名男生,记他们的身高分别为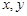 ,求满足:
,求满足: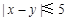 的事件的概率.
的事件的概率.
已知函数 ,记数列
,记数列 的前
的前 项和为
项和为 ,
, ,当
,当 时,
时,
(1)计算 、
、 、
、 、
、 ;
;
(2)猜想 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(3)求证: …
…
在平面直角坐标系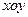 中,经过点
中,经过点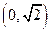 且斜率为
且斜率为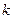 的直线
的直线 与椭圆
与椭圆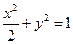 有两个不同的交点
有两个不同的交点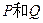 。
。
(1)求实数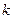 的取值范围;
的取值范围;
(2)设椭圆与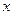 轴正半轴,
轴正半轴,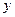 轴正半轴的交点分别为
轴正半轴的交点分别为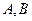 ,是否存在常数
,是否存在常数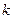 ,使得向量
,使得向量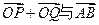 共线?如果存在,求
共线?如果存在,求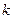 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
若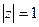 ,且
,且 为负实数,求复数
为负实数,求复数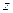 .
.
(本小题满分13分)
已知数列 满足:
满足: ,
,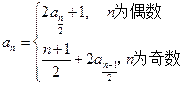

(I)求 得值;
得值;
(II)设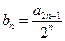 ,试求数列
,试求数列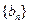 的通项公式;
的通项公式;
(III)对任意的正整数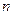 ,试讨论
,试讨论 与
与 的大小关系。
的大小关系。
(本小题满分13分)
已知椭圆C的对称中心为原点O,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为 ,且
,且 =2点
=2点 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过 的直线
的直线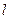 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若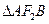 的面积为
的面积为 ,求以
,求以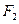 为圆心且与直线
为圆心且与直线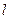 相切的圆的方程。
相切的圆的方程。