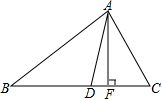
阅读下面的材料：
小明遇到一个问题：如图（1）,在□ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.如果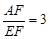
,求
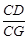的值.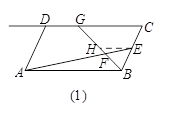 
他的做法是：过点E作EH∥AB交BG于点H,则可以得到△BAF∽△HEF.
请你回答：（1）AB和EH的数量关系为 ,CG和EH的数量关系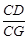为 ,的值为 .
（2）如图（2）,在原题的其他条件不变的情况下,如果
,那么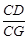的值为 （用含a的代数式表示）.
（3）请你参考小明的方法继续探究：如图（3）,在四边形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F. 如果
,那么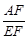
的值为 （用含m,n的代数式表示）.
如图，已知D是△ABC的边AC上的一点，且CD=2AD，AE⊥BC于E，若BC=13，△BDC的面积是39，求AE的长．
如图，在△ABC中，∠A=40°，∠B=72°，CD是AB边上的高；CE是∠ACB的平分线，DF⊥CE于F，求∠BCE和∠CDF的度数．
某开发区有一空地ABCD，如图所示，现计划在空地上种草皮，经测量，∠B=90°，AB=3m，BC=4m，AD=12m，CD=13m，若每种植1平方米草皮需要100元，问总共需要投入多少元？
在等边△ABC中，D是AC的中点，E是BC延长线上一点，且CE=CD，
（1）请说明DB=DE的理由．
（2）若等边△ABC的边长为4cm，求△BDE的面积．
如图，四边形ABCD中，AD∥BC，AC与BD相交于点O，
（1）△ABC与△DBC的面积相等吗？为什么？
（2）若S△AOB=21cm2，求S△COD；
（3）若S△AOD=10cm2，且BO：OD=2：1，求S△ABD．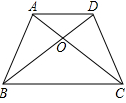
（1）根据已知得出∴△ABC的边BC上的高和△DBC边BC上的高相等，设此高为h，根据三角形的面积公式求出即可；
（2）根据△ABC的面积和△DBC的面积相等，都减去△OBC的面积，即可得出△AOB的面积和△DOC的面积相等；
（3）求出BD=3OD，根据面积公式代入求出即可．
解：（1））△ABC与△DBC的面积相等，理由是：
∵AD∥BC，
∴△ABC的边BC上的高和△DBC边BC上的高相等，设此高为h，
∴△ABC的面积是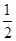
BC×h，△DBC的面积是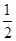×BC×h，
∵BC=BC，
∴△ABC与△DBC的面积相等；
（2）∵S△ABC=S△DBC，
∴S△ABC﹣S△OBC=S△DBC﹣S△OBC，
∴S△AOB=S△DOC=21cm2，
即S△COD=21cm2；
（3）∵BO：OD=2：1，
∴BD=3OD，
∵△AOD的边OD上的高和△ABD的边BD上的高相等，设此高为a，
∵S△AOD=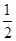×OD×a=10cm2，
∴S△ABD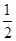．=×BD×a=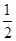×3OD×a=3×10cm2=30cm2．
【题目】
如图，AF是△ABC的高，AD是△ABC的角平分线，且∠B=38°，∠C=72°，求∠DAF的度数．