若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤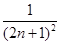 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<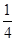 .
.
请给以下各图分类.
某地区为响应上级号召,在2011年初,新建了一批有200万平方米的廉价住房,供困难的城市居民居住.由于下半年受物价的影响,根据本地区的实际情况,估计今后住房的年平均增长率只能达到5%.
(1)经过x年后,该地区的廉价住房为y万平方米,求y=f(x)的表达式,并求此函数的定义域.
(2)作出函数y=f(x)的图象,并结合图象求:经过多少年后,该地区的廉价住房能达到300万平方米?
物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t后的温度是T,则T-Ta=(T0-Ta)·( )
)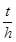 ,其中Ta表示环境温度,h称为半衰期.现有一杯用88 ℃热水冲的速溶咖啡,放在24 ℃的房间中,如果咖啡降温到40 ℃需要20 min,那么降温到35 ℃时,需要多长时间?
,其中Ta表示环境温度,h称为半衰期.现有一杯用88 ℃热水冲的速溶咖啡,放在24 ℃的房间中,如果咖啡降温到40 ℃需要20 min,那么降温到35 ℃时,需要多长时间?
某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.
(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数v=5log2 ,单位是m/s,其中Q表示燕子的耗氧量.
,单位是m/s,其中Q表示燕子的耗氧量.
(1)试计算:燕子静止时的耗氧量是多少个单位?
(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少?