如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,O为AC与BD的交点,E为PB上任意一点.
(1)证明:平面EAC⊥平面PBD;
(2)若PD∥平面EAC,并且二面角B-AE-C的大小为45°,求PD∶AD的值.
 。
。




(理)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC
⊥平面ABC,SA=SC=2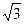 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面CMN的距离.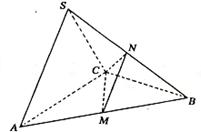
(文)已知两定点
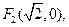 满足条件
满足条件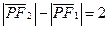 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
(Ⅰ)求k的取值范围;
(Ⅱ)如果 且曲线E上存在点C,使
且曲线E上存在点C,使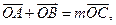 求
求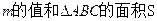 。
。
(理)在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱
AD上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D的大小为 。
。