如图,在矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将△AOD折起,使DB=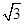 .
.
(1)求证:平面AOD⊥平面ABCO;
(2)求直线BC与平面ABD所成角的正弦值.
如图,在△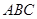 中,∠
中,∠ 是角平分线,
是角平分线, 交
交 于
于 ⊙
⊙ 是△
是△ 的外接圆。
的外接圆。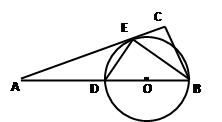
⑴求证: 是⊙
是⊙ 的切线;
的切线;
⑵如果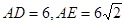 ,求
,求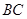 的长。
的长。
已知
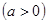
⑴若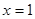 是
是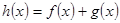 的极值点,求实数
的极值点,求实数 值。
值。
⑵若对 都有
都有 成立,求实数
成立,求实数 的取值范围。
的取值范围。
已知点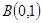 ,点
,点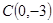 ,直线
,直线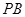 、
、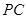 都是圆
都是圆 的切线(
的切线(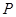 点不在
点不在 轴上)。
轴上)。
⑴求过点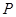 且焦点在
且焦点在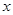 轴上抛物线的标准方程;
轴上抛物线的标准方程;
⑵过点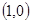 作直线
作直线 与⑴中的抛物线相交于
与⑴中的抛物线相交于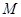 、
、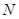 两点,问是否存在定点
两点,问是否存在定点 ,使
,使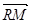 .
. 为常数?若存在,求出点
为常数?若存在,求出点 的坐标与常数;若不存在,请说明理由。
的坐标与常数;若不存在,请说明理由。
一学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为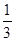 ,参加第五项不合格的概率为
,参加第五项不合格的概率为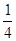 。
。
⑴求该生被录取的概率;
⑵记该生参加考试的项数为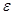 ,求
,求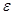 的分布列和期望。
的分布列和期望。
一个多面体的直观图和三视图如图所示,其中 、
、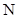 分别是
分别是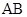 、
、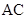 的中点,
的中点,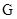 是
是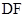 上的一动点,主视图与俯视图都为正方形。
上的一动点,主视图与俯视图都为正方形。

⑴求证: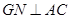 ;
;
⑵当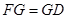 时,在棱
时,在棱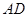 上确定一点
上确定一点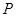 ,使得
,使得 ∥平面
∥平面 ,并给出证明。
,并给出证明。
⑶求二面角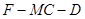 的平面角余弦值。
的平面角余弦值。