如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.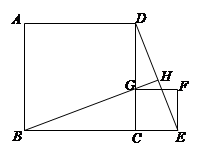
(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)说明:∠O=∠BEO+∠DFO.
(2)如图2,如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.
(3)若将折线继续折下去,折三次,折四次折n次,又会得到怎样的结论?(不需证明)
某蔬菜公司收购到某种蔬菜280吨,准备加工后上市销售.该公司的加工能力是:每天可以精加工12吨或者粗加工32吨.现计划用15天完成加工任务,该公司应安排几天粗加工,几天精加工,才能按期完成任务?如果每吨蔬菜粗加工后的利润为1500元,精加工后为3000元,那么该公司出售这些加工后的蔬菜共可获利多少元?
如图,M、N、T和P、Q、R分别在同一直线上,且∠1=∠3,∠P=∠T,说明∠M=∠R的理由
如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
如图,有一条小船.小船移动过程以点A的位置变化为参照。
(1)若把小船平移,使点A移到点B,请你在图中画出平移后的小船.
(2)若该小船先从点A航行到达岸边L的点P(即A点与L上的P点重合)处补给后,再航行到点B,但要求航程最短,试在图中画出点P的位置
(3)求出靠岸点P与A,B所围成的△ABP的面积.(简要写出计算过程即可)