如图,M、N、T和P、Q、R分别在同一直线上,且∠1=∠3,∠P=∠T,说明∠M=∠R的理由
在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园 ,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的
,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的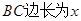 (m),花园的面积为
(m),花园的面积为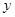 (m
(m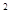 ).
).
(1)求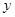 与
与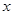 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量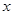 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m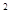 吗?若能,求出此时
吗?若能,求出此时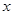 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当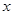 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?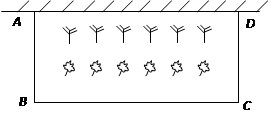
如图,在平行四边形ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1cm的速度匀速运动,在BC上以每秒2cm的速度匀速运动.过Q作直线QN,使QN∥PM.设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为Scm2.
①求S关于t的函数关系式;
②(附加题)求S的最大值.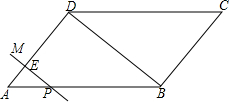
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量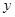 (万件)与销售单位
(万件)与销售单位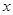 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求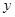 关于
关于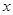 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利 (万元)关于销售单价
(万元)关于销售单价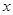 (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价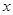 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
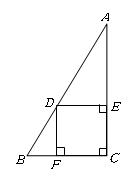
如图,在Rt△ 中,
中,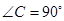 ,
,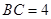 ,
,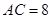 ,点
,点 在斜边
在斜边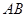 上,分别作
上,分别作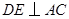 于
于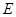 ,
, 于
于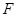 ,设
,设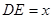 ,
,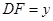 .
.
(1)求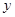 与
与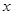 之间的函数关系,并求出
之间的函数关系,并求出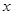 的取值范围.
的取值范围.
(2)设四边形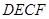 的面积为
的面积为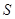 ,试求
,试求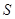 的最大值.
的最大值.
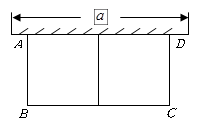
如图,有长为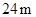 的篱笆,现一面利用墙(墙的最大可用长度
的篱笆,现一面利用墙(墙的最大可用长度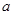 为
为 )围成中间隔有一道篱笆的长方形花圃,设花圃的宽
)围成中间隔有一道篱笆的长方形花圃,设花圃的宽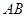 为
为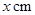 ,面积为
,面积为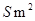 .
.
(1)求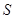 与
与 的函数关系式.
的函数关系式.
(2)要围成面积为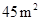 的花圃,
的花圃,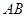 的长是多少米?
的长是多少米?
(3)能围成面积比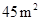 还大的花圃吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.
还大的花圃吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.