如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.
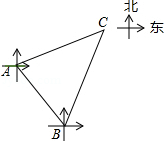
如图,建筑物 在观测点 的北偏东 方向上,从观测点 出发向南偏东 方向走了 到达观测点 ,此时测得建筑物 在观测点 的北偏东 方向上,求观测点 与建筑物 之间的距离.(结果精确到 .参考数据:
为增强学生环保意识,某中学举办了环保知识竞赛,某班共有5名学生 名男生,2名女生)获奖.
(1)老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为 .
(2)老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.
某校要了解学生每天的课外阅读时间情况,随机调查了部分学生,对学生每天的课外阅读时间 (单位: 进行分组整理,并绘制了如图所示的不完整的统计图表,根据图中提供的信息,解答下列问题:
(1)本次调查共抽取 名学生.
(2)统计表中 , .
(3)将频数分布直方图补充完整.
(4)若全校共有1200名学生,请估计阅读时间不少于 的有多少人.
|
课外阅读时间 |
频数 人 |
频率 |
|
|
6 |
0.1 |
|
|
12 |
0.2 |
|
|
|
0.25 |
|
|
18 |
|
|
|
9 |
0.15 |

如图,四边形 为平行四边形, 和 的平分线 , 分别交 , 的延长线于点 , ,交边 , 于点 , .
(1)求证:四边形 是平行四边形.
(2)若 , ,求 的值.

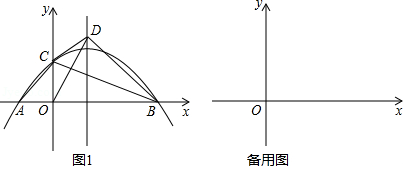
在平面直角坐标系中,抛物线 过点 , ,与 轴交于点 ,连接 , ,将 沿 所在的直线翻折,得到 ,连接 .
(1)用含 的代数式表示点 的坐标.
(2)如图1,若点 落在抛物线的对称轴上,且在 轴上方,求抛物线的解析式.
(3)设 的面积为 , 的面积为 ,若 ,求 的值.