已知函数f(x)= (A>0,
(A>0, >0,
>0, )的图象的一部分如下图所示.
)的图象的一部分如下图所示.
(1)求函数f(x)的解析式.
(2)当x (-6,2)时,求函数g(x)= f(x+2)的单调递增区间.
(-6,2)时,求函数g(x)= f(x+2)的单调递增区间.
.已知关于x的一元二次方程x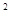 -2(a-2)x-b
-2(a-2)x-b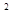 +16=0.
+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
有一个容量为100的样本,数据的分组及各组的频数如下: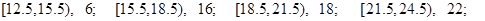
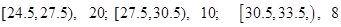
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息?(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
.设计一个求关于x的方程a x + b = 0的解的算法和程序框图