已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
如图,三角形ABC中,AC=BC= ,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(1)求证:GF//底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.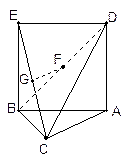
广雅中学在高二年级开设了 ,
, ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
, ,
,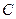 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 |
小组人数 |
抽取人数 |
 |
24 |
 |
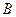 |
36 |
3 |
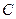 |
48 |
 |
(1)求 ,
, 的值;
的值;
(2)若从 ,
,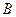 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组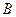 的概率.
的概率.
设函数y= 是定义在(0,+∞)上的增函数,并满足
是定义在(0,+∞)上的增函数,并满足
1、求f(1)的值;
2、若存在实数m,使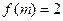 ,求m的值
,求m的值
3、如果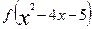 <2求x的范围
<2求x的范围
已知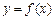 是定义在R上的函数,对于任意的
是定义在R上的函数,对于任意的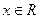 ,
, ,且当
,且当 时,
时,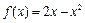 .
.
(1)求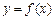 的解析式;
的解析式;
(2)画出函数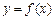 的图象,并指出
的图象,并指出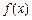 的单调区间及在每个区间上的增减性;
的单调区间及在每个区间上的增减性;
(3)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围. 
已知函数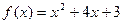 ,
,
(1)若 为偶函数,求
为偶函数,求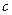
(2)证明:函数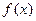 在区间
在区间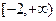 上是增函数。
上是增函数。