某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数.
(1)根据茎叶图计算样本均值；
(2)日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？
(3)从该车间12名工人中，任取2人，求恰有1名优秀工人的概率．
已知函数f(x)＝x2＋4ax＋2a＋6.
(1)若函数f(x)的值域为[0，＋∞)，求a的值；
(2)若函数f(x)的函数值均为非负数，求g(a)＝2－a|a＋3|的值域．
已知集合A＝{x∈R|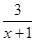
≥1}，集合B＝{x∈R|y＝
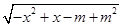}，若A∪B＝A，求实数m的取值范围．
设函数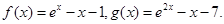
解不等式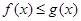
；
事实上：对于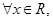
有
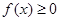成立，当且仅当
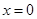时取等号.由此结论证明:
.
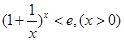如图，AB是圆的直径，PA垂直圆所在的平面，C是圆周上的一点．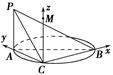
（1）求证：平面PAC⊥平面PBC；(6分)
（2）若AB＝2，AC＝1，PA＝1，求二面角CPBA的余弦值．
已知函数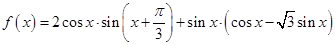
（1）求函数
的最小正周期和单调递减区间；；
（2）在
中，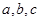
分别是角A、B、C的对边，若
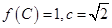,求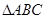面积的最大值．