已知函数f(x)=2cos (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈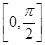 ,f
,f =-
=-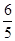 ,f
,f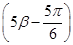 =
=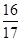 ,求cos(α+β)的值.
,求cos(α+β)的值.
(本小题满分12分)
在△ABC中,内角A、B、C的对边分别为a、b、c,D、E分别为AB、BC的中点,且 ·
· =
=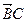 ·
·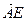 。
。
(1)求证: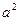 ,
, ,
,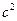 成等差数列;
成等差数列;
(2)求 B及sinB+cosB的取值范围
B及sinB+cosB的取值范围
(本小题满分12分)
已知函数
 ,其图象过点(
,其图象过点( ,
, ).
).
(1)求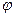 的值及
的值及 最小正周期;
最小正周期;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.
(本小题满分10分)
已知等差数列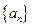 满足:
满足: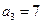 ,
,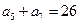 .
.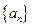 的前n项和为
的前n项和为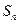 .
.
(1)求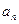 及
及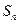 ;
;
(2)令bn=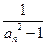 (n
(n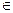 N*),求数列
N*),求数列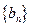 的前n项和
的前n项和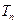
(本小题满分10分)
平面向量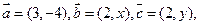 已知
已知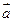 ∥
∥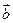 ,
,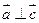 ,求
,求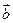 、
、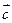 及
及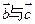 夹角.
夹角.
已知圆 的圆心为N,一动圆与这两圆都外切。
的圆心为N,一动圆与这两圆都外切。
(1)求动圆圆心 的轨迹方程;
的轨迹方程;
(2)若过点N的直线L与(1)中所求轨迹有两交点A、B,求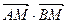 的取值范围
的取值范围