正项数列{an}的前n项和Sn满足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求数列{an}的通项公式an;
(2)令bn=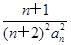 ,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<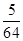 .
.
(本小题满分12分)设数列 的通项公式为
的通项公式为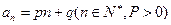 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,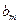 是使得不等式
是使得不等式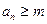 成立的所有n中的最小值.(1)若
成立的所有n中的最小值.(1)若 ,求
,求 ;(2)若
;(2)若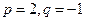 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得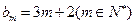 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分12分)已知椭圆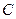 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点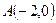 ,离心率
,离心率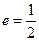 ,
,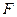 为右焦点,过焦点
为右焦点,过焦点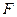 的直线交椭圆
的直线交椭圆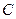 于
于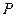 、
、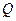 两点(不同于点
两点(不同于点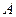 ).(1)求椭圆
).(1)求椭圆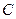 的方程;(2)当
的方程;(2)当 时,求直线PQ的方程;(3)判断
时,求直线PQ的方程;(3)判断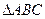 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.
(本小题满分13分)设函数 .(1)求
.(1)求 的最小正周期(2)若函数
的最小正周期(2)若函数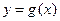 与
与 的图像关于直线
的图像关于直线 对称,求当
对称,求当 时
时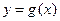 的最大值.
的最大值.
(本小题满分13分)设函数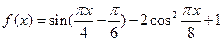 .(1)求
.(1)求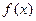 的最小正周期(2)若函数
的最小正周期(2)若函数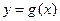 与
与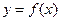 的图像关于直线
的图像关于直线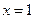 对称,求当
对称,求当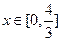 时
时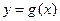 的最大值.
的最大值.
(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为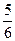 和
和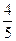 ,且各株大树是否成活互不影响。求移栽的4株大树中:
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。