已知向量a＝(Asin ωx，Acos ωx)，b＝(cos θ，sin θ)，f(x)＝a·b＋1，其中A>0，ω>0，θ为锐角．f(x)的图象的两个相邻对称中心的距离为
，且当x＝
时，f(x)取得最大值3.
(1)求f(x)的解析式；
(2)将f(x)的图象先向下平移1个单位，再向左平移φ(φ>0)个单位得g(x)的图象，若g(x)为奇函数，求φ的最小值．
如图，有一块抛物线形钢板，其下口宽为 2 米 ，高为 2米.计划将此钢板
切割成等腰梯形的形状，下底AB是抛物线的下口，上底CD的端点在抛物线上，
(1) 请建立适当的直角坐标系，求抛物线形钢板所在抛物线方程;
（2）记CD =" 2" x ，写出梯形面积S 以 x 为自变量的函数式，并指出定义域;
（3）求面积S的最大值.
 |
（本小题满分10分）
已知函数
在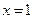
处的切线方程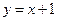
（1）求a，b的值；
（2）求函数
在 
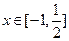值域.
已知椭圆焦点是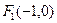 
和
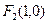，离心率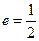 
（1）求椭圆的标准方程;
（2）设点
在这个椭圆上，且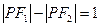
，求 
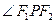的余弦值.
已知某物体的位移
（米）与时间
（秒）的关系是
，
（1）求
秒到
秒的平均速度；
（2）求此物体在
秒的瞬时速度.
(本小题13分)
已知椭圆的焦点在
轴上，它的一个顶点恰好是抛物线
的焦点，离心率
，过椭圆的右焦点
作不与坐标轴垂直的直线
，交椭圆于A、B两点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设点M（m，0）是线段OF上的一个动点，且
，求
取值范围；
（Ⅲ）设点C是点A关于x轴的对称点，在x轴上是否存在一个定点N，使得C、B、N 三点共线？若存在，求出定点N的坐标，若不存在，请说明理由．