已知直线l:y=x+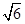 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: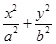 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=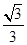 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两条切线的斜率之积为定值.
二次函数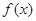 满足
满足 且
且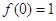 .
.
1.求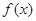 的解析式;
的解析式;
2.在区间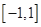 上,
上,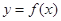 的图象恒在
的图象恒在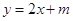 的图象上方,试确定实数m的范围.
的图象上方,试确定实数m的范围.
已知函数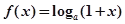 ,
,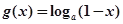 ,其中
,其中 ,设
,设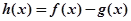 .
.
(1)求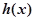 的定义域,并判断奇偶性,说明理由;
的定义域,并判断奇偶性,说明理由;
(2)若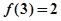 ,求使
,求使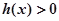 成立的x的集合.
成立的x的集合.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
(1)求这个奖杯的体积( 取
取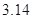 );
);
(2)求这个奖杯底座的侧面积.
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若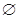
 A∩B,A∩C=
A∩B,A∩C=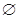 ,求a的值
,求a的值
设函数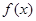 是定义在
是定义在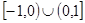 上的奇函数,当
上的奇函数,当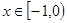 时,
时,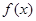
 为实数);
为实数);
(1)当 时,求函数
时,求函数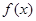 的解析式;
的解析式;
(2)若 ,试判断
,试判断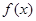 在
在 上的单调性;
上的单调性;
(3)是否存在a,使得当 时,
时,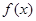 有最大值
有最大值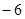 。
。