有形状、大小和质地都相同的四张卡片,正面分别写有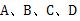 和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A、B、C、D表示);
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜,若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利,为什么?
某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成下两幅统计图(如图),请你结合图中所给信息解答下列问题:(说明:A级:90分—100分;B级:75分—89分;C级:60分—74分;D级:60分以下)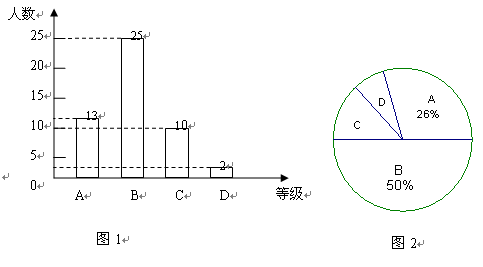
(1)D级学生的人数占全班人数的百分比为▲;
(2)扇形统计图中C级所在扇形圆心角度数为▲;
(3)该班学生体育测试成绩的中位数落在等级▲内;
(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为2000千克/亩、2500千克/亩,收购单价分别是8元/千克、7元/千克.(1)若该基地全年收获A、B两种生姜的年总产量为68000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?
如图,在△ABC中,点E是AC边上的中点,点F是AB边上的中点,连结EF并延长至点D,再连结BD,请你添加一个条件,使BD=CE(不再添加其它线段,不再标注或使用其他字母), 并给出证明,添加的条件是: ▲.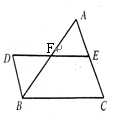
(1)计算:
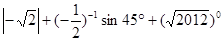 ;
;(2)先化简,再求值:
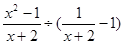 ,其中
,其中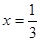 ·
·
如图,在平面直角坐标系中,直角梯形 的边
的边 落在
落在 轴的正半轴上,且
轴的正半轴上,且 ∥
∥ ,
, ,
, =4,
=4, =6,
=6, =8.正方形
=8.正方形 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积。将正方形
面积。将正方形 沿
沿 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为 。
。(1)分析与计算:
求正方形 的边长;
的边长;(2)操作与求解:
①正方形 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断 (
( >0)的变化情况是;
>0)的变化情况是;
| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
②当正方形 顶点
顶点 移动到点
移动到点 时,求
时,求 的值;
的值;(3)探究与归纳:
设正方形 的顶点
的顶点 向右移动的距离为
向右移动的距离为 ,求重叠部分面积
,求重叠部分面积 与
与 的函数关系式。
的函数关系式。