已知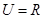 ,
, ,
,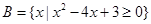 ,求:
,求:
(1) (2)
(2)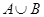 (3)
(3)
已知O为平面直角坐标系的原点,设 =(2,5),
=(2,5),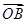 =(3,1),
=(3,1),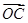 =(6,3).在线段OC上是否存在点M,使MA⊥MB.若存在,求出点M的坐标;若不存在,请说明理由.
=(6,3).在线段OC上是否存在点M,使MA⊥MB.若存在,求出点M的坐标;若不存在,请说明理由.
如图所示,已知△ABC中,A(2,-1),B(3,2),C(-3,-1),AD是BC边上的高,求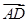 及点D的坐标.
及点D的坐标.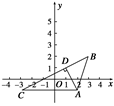
已知a=(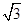 ,-1),b=
,-1),b= .
.
(1)求证:a⊥b;
(2)若存在不同时为0的实数k和t,使x=a+(t-3)b,y=-ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)求函数k=f(t)的最小值.
已知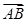 =(6,1),
=(6,1),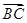 =(x,y),
=(x,y),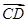 =(-2,-3),若
=(-2,-3),若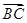 ∥
∥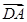 ,
,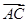 ⊥
⊥ .
.
(1)求x、y的值;
(2)求四边形ABCD的面积.