已知椭圆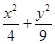 =1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且
=1上任一点P,由点P向x轴作垂线PQ,垂足为Q,设点M在PQ上,且 =2
=2 ,点M的轨迹为C.
,点M的轨迹为C.
(1)求曲线C的方程;
(2)过点D(0,-2)作直线l与曲线C交于A、B两点,设N是过点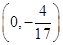 且平行于x轴的直线上一动点,且满足
且平行于x轴的直线上一动点,且满足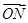 =
= +
+ (O为原点),且四边形OANB为矩形,求直线l的方程.
(O为原点),且四边形OANB为矩形,求直线l的方程.
(本小题满分14分)
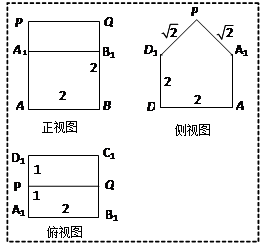
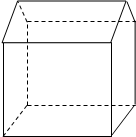
如图,已知几何体的三视图(单位:cm).
(1)在这个几何体的直观图相应的位置标出字母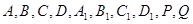 ;
;
(2)求这个几何体的表面积及体积;
(3)设异面直线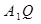 、
、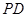 所成角为
所成角为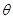 ,求
,求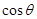 .
.
已知命题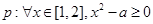 .命题
.命题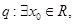 使得
使得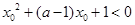 ;若“
;若“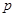 或
或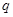 为真,
为真,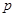 且
且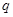 为假”,求实数
为假”,求实数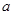 的取值范围.
的取值范围.
(本小题满分12分)
已知函数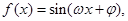 其中
其中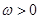 ,
,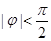
(I)若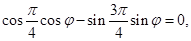 求
求 的值;
的值;
(Ⅱ)在(I)的条件下,若函数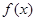 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于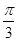 ,
,
①求函数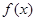 的解析式;②求最小正实数
的解析式;②求最小正实数 ,使得函数
,使得函数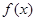 的图象向左平移
的图象向左平移 个单位时对应的函数是偶函数.
个单位时对应的函数是偶函数.
设函数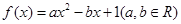 ,
,
(1)如果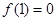 且对任意实数
且对任意实数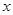 均有
均有 ,求
,求 的解析式;
的解析式;
(2)在(1)在条件下, 若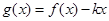 在区间
在区间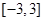 是单调函数,求实数
是单调函数,求实数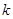 的取值范围;
的取值范围;
(3)已知 且
且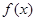 为偶函数,如果
为偶函数,如果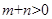 ,求证:
,求证: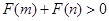 .
.
已知函数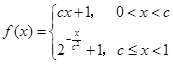 满足
满足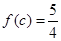 .
.
(1)求常数 的值;
的值;
(2)求使 成立的x的取值范围.
成立的x的取值范围.