设函数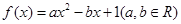
，
(1) 如果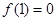
且对任意实数
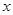均有
,求
的解析式；
(2) 在(1)在条件下, 若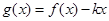
在区间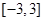
是单调函数,求实数
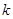的取值范围；
(3) 已知
且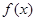
为偶函数，如果
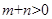，求证：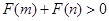
．
数列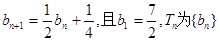
的前n项和。
（1）求证：数列
是等比数列，并求
的通项公式；
（2）如果对任意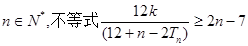
恒成立，求实数k的取值范围。
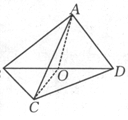
如图所示，已知正方形ABCD的边长为2，AC∩BD=O，将正方形ABCD沿对角线BD折起，得到三棱锥A—BCD。
（1）求证：平面AOC⊥平面BCD；
（2）若三棱锥A—BCD的体积为
，求AC的长。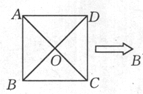
某电视台的一个智力游戏节目中，有一道将中国四大名著《三国演义》、《水浒传》、《西游记》、《红楼梦》与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线，每连对一个得2分，连错得-1分，某观众只知道《三国演义》的作者是罗贯中，其它不知道随意连线，将他的得分记作ξ。
（1）求该观众得分ξ为负数的概率；
（2）求ξ的分布列及数学期望。
已知在△ABC中，角A、B、C所对的边分别为a，b，c，且
。
（1）求角B的大小；
（2）设向量
取最大值时，tanC的值。
已知方程
。求使方程有两个大于1的实数根的充要条件。