设袋子中装有a个红球,b个黄球,c个蓝球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个蓝球得3分.
(1)当a=3,b=2,c=1时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量ξ为取出此2球所得分数之和,求ξ的分布列;
(2)从该袋子中任取(每球取到的机会均等)1个球,记随机变量η为取出此球所得分数.若E(η)=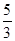 ,D(η)=
,D(η)= ,求a∶b∶c.
,求a∶b∶c.
(满分12分)已知命题 上
上 有且仅有一解;命题
有且仅有一解;命题 只有一个实数
只有一个实数 满足不等式
满足不等式 .若命题“
.若命题“ ”是假命题,求实数
”是假命题,求实数 的取值范围.
的取值范围.
满分10分) 设有关于 的一元二次方程
的一元二次方程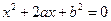
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从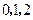 三个数中任取的一个数,求上述方程有实根的概率
三个数中任取的一个数,求上述方程有实根的概率
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率
任取的一个数,求上述方程有实根的概率
(本小题满分14分)
已知函数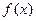 对一切实数x,y都有
对一切实数x,y都有 成立,且
成立,且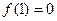 .
.
(1)求 的值
的值
(2)求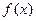 的解析式
的解析式
(3)若 ,对任意的
,对任意的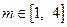 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围
(本小题满分12分)
已知二次函数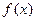 满足
满足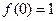 ,及
,及 .
.
(1)求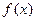 的解析式;
的解析式;
(2)若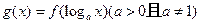 ,
,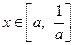 ,试求
,试求 的值域.
的值域.
(本小题满分12分) 函数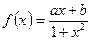 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且
(1)求函数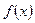 的解析式
的解析式
(2)利用定义证明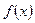 在(-1,1)上是增函数
在(-1,1)上是增函数
(3)求满足 的
的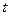 的范围
的范围