.如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将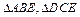 折起,使得B\C重合于O.
折起,使得B\C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD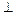 AO;.
AO;.
(Ⅱ)求二面角O—AE—D的余弦值.
一个盒子中装有大小相同的小球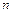 个,在小球上分别标有1,2,3,
个,在小球上分别标有1,2,3,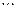 ,
,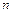 的号码,已知从盒子中随机的取出两个球,两球的号码最大值为
的号码,已知从盒子中随机的取出两个球,两球的号码最大值为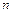 的概率为
的概率为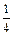 ,
,
(Ⅰ)问:盒子中装有几个小球?
(Ⅱ)现从盒子中随机的取出4个球,记所取4个球的号码中,连续自然数的个数的最大值为随机变量 (如取2468时,
(如取2468时, =1;取1246时,
=1;取1246时, =2,取1235时,
=2,取1235时, =3),
=3),
(ⅰ)求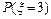 的值;(ⅱ)求随机变量
的值;(ⅱ)求随机变量 的分
的分 布列及均值.
布列及均值.
已知:向量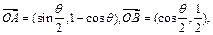 (O为坐标原点).
(O为坐标原点).
(Ⅰ)求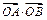 的最大值及此时
的最大值及此时 的值组成的集合;
的值组成的集合;
(Ⅱ)若A点在直线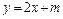 上运动,求实数
上运动,求实数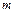 的取值范围.
的取值范围.
((本小题满分14分)
已知函数 .
.
(1)当 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围;
(2)当 时,试比较
时,试比较 与
与 的大小;
的大小;
(3)求证: (
( ).
).
(本小题满分14分)
已知数列 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和,且满足
项和,且满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前n项和.
的前n项和.
(1)求 、
、 和
和 ;
;
(2)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.