某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| |
专业A |
专业B |
总计 |
| 女生 |
12 |
4 |
16 |
| 男生 |
38 |
46 |
84 |
| 总计 |
50 |
50 |
100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=
| P(K2≥k0) |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k0 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
设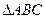 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3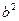 +3
+3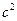 -3
-3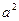 =4
=4 bc .
bc .
(Ⅰ) 求sinA的值;
(Ⅱ)求 的值.
的值.
(本小题满分14分)设函数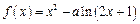 (
( ,
,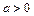 ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时 的值,并证明你的结论.
的值,并证明你的结论.
(本题14分)用长度为18cm的钢条围成一个长方体形状的框架,要求长方体的长和宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积为多少?
(本题14分)已知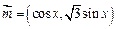 ,
, ,设
,设 .
.
(1)求函数 的图像的对称轴及其单调递增区间;
的图像的对称轴及其单调递增区间;
(2)当 ,求函数
,求函数 的值域及取得最大值时
的值域及取得最大值时 的值;
的值;
(3)若 分别是锐角
分别是锐角 的内角
的内角 的对边,且
的对边,且 ,
,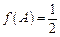 ,试求
,试求 的面积
的面积 .
.
(本题14分)已知函数
(1)讨论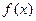 的单调区间;
的单调区间;
(2)若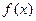 在
在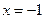 处取得极值,直线y=m与
处取得极值,直线y=m与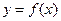 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。