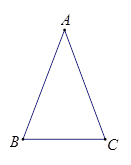
通过锐角三角比的学习，我们已经知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长比与角的大小之间可以相互转化. 类似的我们可以在等腰三角形中建立边角之间的联系.我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）. 如下图在△ABC中，AB=AC,顶角A的正对记作sadA，这时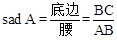
. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义，解下列问题：
（1）sad60º=_____________；sad90º=________________。
（2）对于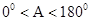
，
的正对值sadA的取值范围是_____________。
（3）试求sad36º的值.
抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.
(1)求此抛物线的解析式；
(2)抛物线上是否存在点P,使
,若存在，求出P点坐标；若不存在，请说明理由.
已知二次函数y=ax2-4x+c的图象过点（-1，0）和点（2，-9）．
（1）求该二次函数的解析式并写出其对称轴；
（2）已知点P（2，-2），连结OP，在x轴上找一点M，使△OPM是等腰三角形，请直接写出点M的坐标（不写求解过程）．
如图，在
中，以
为直径的
交
于点
，点
为
的中点，连结
交于点
，且
.
（1）判断直线
与⊙O的位置关系，并证明你的结论；
（2）若的半径为2,
,求的长.
如图,已知二次函数y=x
－4x+3的图象交x轴于A，B两点（点A在点B的左侧），交y轴于点C.
（1）求直线BC的解析式；
（2）点D是在直线BC下方的抛物线上的一个动点，当△BCD的面积最大时，求D点坐标.
如图，在平面直角坐标系xOy中，点A的坐标为（﹣2，0），等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD．
（1）△AOC沿x轴向右平移得到△OBD，则平移的距离是个单位长度；
（2）△AOC与△BOD关于直线对称，则对称轴是；
（3）△AOC绕原点O顺时针旋转可以得到△DOB，则旋转角度是度，在此旋转过程中，△AOC扫过的图形的面积是．