已知数列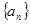 是等差数列,
是等差数列,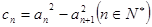
(1)判断数列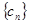 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果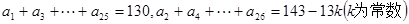 ,试写出数列
,试写出数列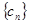 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列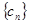 得前n项和为
得前n项和为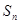 ,问是否存在这样的实数
,问是否存在这样的实数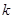 ,使
,使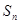 当且仅当
当且仅当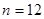 时取得最大值。若存在,求出
时取得最大值。若存在,求出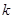 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(本题10分)已知函数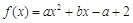 .
.
(1)若关于x的不等式 的解集是
的解集是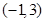 ,求实数
,求实数 的值;
的值;
(2)若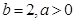 ,解关于x的不等式
,解关于x的不等式 .
.
(本题12分)已知数列 满足
满足
(1)求数列 的通项公式;
的通项公式;
(2)若数列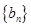 满足
满足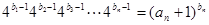 ,证明:
,证明: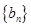 是等差数列;
是等差数列;
(3)证明:
(本小题满分10分)某商店根据以往某种新产品的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.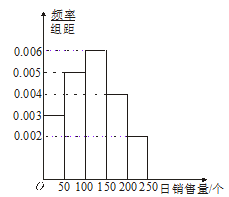
(1)估计日销售量的众数;
(2)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(3)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列.
(本小题满分10分) 展开式第
展开式第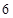 项与第
项与第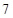 项的系数相等,求展开式中二项式系数最大项和系数最大项.
项的系数相等,求展开式中二项式系数最大项和系数最大项.
(本小题满分10分)盒中有大小相同的编号为1,2,3,4,5,6的6只小球,规定:从盒中一次摸出两只球,如果这两只球的编号均能被3整除,则获得一等奖,奖金10元,如果这两只球的编号均为偶数,则获得二等奖,奖金2元,其他情况均不获奖.
(1)若某人参加摸球游戏一次获奖金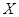 元,求
元,求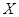 的分布列;
的分布列;
(2)若某人摸一次且获奖,求他获得一等奖的概率.