已知函数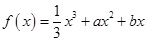
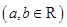 .
.
(1)若曲线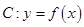 经过点
经过点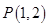 ,曲线
,曲线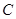 在点
在点 处的切线与直线
处的切线与直线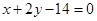 垂直,求
垂直,求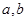 的值;
的值;
(2)在(1)的条件下,试求函数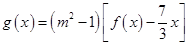 (
(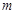 为实常数,
为实常数,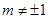 )的极大值与极小值之差;
)的极大值与极小值之差;
(3)若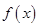 在区间
在区间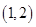 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: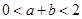 .
.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前 吨甲产品能耗为
吨甲产品能耗为 吨标准煤;试根据(2)求出的线性回归方程,预测生产
吨标准煤;试根据(2)求出的线性回归方程,预测生产 吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
已知中心在原点,一焦点为 的椭圆被直线
的椭圆被直线 截得的弦的中点横坐标为
截得的弦的中点横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)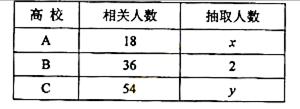
(1)求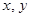 ;
;
(2)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。
已知命题p: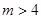 ;命题q:方程
;命题q:方程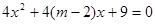 有实根.若
有实根.若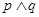 为真,求实数m的取值范围.
为真,求实数m的取值范围.
已知F1、F2分别是椭圆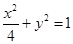 的左、右焦点.
的左、右焦点.
(Ⅰ)若P是第一象限内该图形上的一点,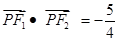 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠AOB为锐角(其中O为作标原点),求直线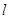 的斜率
的斜率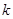 的取值范围.
的取值范围.