经市场调查，某旅游城市在过去的一个月内(以30天计)，旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)＝4＋
，人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)＝115－|t－15|.
(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30，t∈N*)的函数关系式；
(2)求该城市旅游日收益的最小值(万元)．
(本题满分12分)已知
,周长为14，
,求顶点
的轨迹方程.
(本题满分12分)
在等差数列{an}中，若a2＋a3＋a4＋a5＝34，且a2·a5＝52．求数列{an}的通项公式an．
已知抛物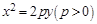线
与直线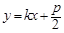
交于A、B两点，O为坐标原点．
（I）当k=1时，求线段AB的长；
（II）当k在R内变化时，求线段AB中点C的轨迹方程；
（III）设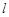
是该抛物线的准线．对于任意实数k，上是否存在点D，使得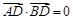
？如果存在，求出点D的坐标；如不存在，说明理由．
如图，四面体ABCD中，O、E分别是BD、BC的中点，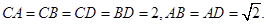
（I）求证：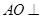
平面BCD；
（II）求点E到平面ACD的距离；
（III）求二面角A—CD—B的余弦值。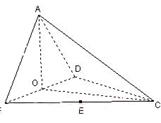
已知a，b，c分别是△ABC的三个内角A、B、C的对边．
（Ⅰ）若△ABC面积为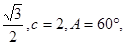
求a，b的值；
（Ⅱ）若acosA=bcosB，试判断△ABC的形状．