已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|;
(3)设函数g(x)= ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
某射手在一次射击中,击中10环、9环、8环的概率分别是0.24、0.28、0.19,求这个射手在一次射击中:
(1)击中10环或9环的概率;
(2)小于8环的概率.
某城市有甲、乙两种报纸供居民们订阅,记事件A:“只订甲报”;事件B:“至少订一种报”,事件C:“至多订一种报”,事件D:“不订甲报”,事件E:“一种报也不订”,判断下列每对事件是不是互斥事件,如果是再判断它们是不是对立事件.
(1)A与C;(2)B与E;(3)B与D;(4)B与C;(5)C与E.
“某彩票的中奖概率为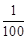 ”,那是否意味着买1000张彩票就中10张奖?
”,那是否意味着买1000张彩票就中10张奖?
从甲地到乙地有A1、A2、A3共3条路线,从乙地到丙地有B1、B2共2条路线,从甲地直接到丙地共4条路线,其中A2B1路线是从甲到丙地的所有路线中最短的一条.某人任选了1条从甲到丙地的路线,它正好是最短路线的概率是多少?
对一批衬衣进行抽检,结果如下表:
| 抽取件数 |
50 |
100 |
200 |
500 |
600 |
700 |
800 |
| 次品件数 |
0 |
20 |
12 |
27 |
27 |
35 |
40 |
| 次品频率 |
0 |
0.20 |
0.06 |
0.054 |
(1)完成上面统计表;
(2)事件A为任取一件衬衣为次品,求P(A);
(3)为了保证买到次品的顾客能够及时更换,销售1000件衬衣,至少需要进货多少件衬衣?