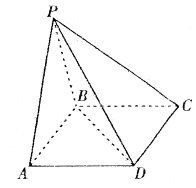
如图,在四棱锥PABCD中,PA⊥底面ABCD,AC⊥CD,∠DAC=60°,AB=BC=AC,E是PD的中点,F为ED的中点.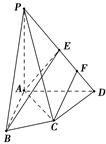
(1)求证:平面PAC⊥平面PCD;
(2)求证:CF∥平面BAE.
已知函数 .
.
(Ⅰ)若函数 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数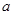 的取值范围;
的取值范围;
(Ⅱ)令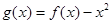 ,是否存在实数
,是否存在实数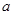 ,当
,当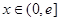 (
(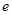 是自然常数)时,函数
是自然常数)时,函数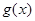 的最小值是3,若存在,求出
的最小值是3,若存在,求出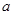 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅲ)当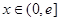 时,证明:
时,证明: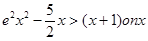
设点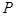 是曲线
是曲线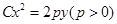 上的动点,点
上的动点,点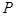 到点(0,1)的距离和它到焦点
到点(0,1)的距离和它到焦点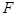 的距离之和的最小值为
的距离之和的最小值为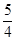 .
.
(1)求曲线C的方程;
(2)若点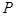 的横坐标为1,过
的横坐标为1,过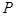 作斜率为
作斜率为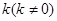 的直线交
的直线交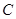 于点
于点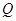 ,交
,交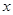 轴于点
轴于点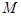 ,过点
,过点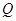 且与
且与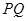 垂直的直线与
垂直的直线与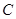 交于另一点
交于另一点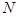 ,问是否存在实数
,问是否存在实数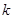 ,使得直线
,使得直线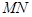 与曲线
与曲线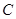 相切?若存在,求出
相切?若存在,求出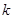 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知等差数列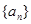 的公差
的公差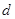 大于0,且
大于0,且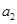 、
、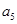 是方程
是方程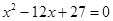 的两根.数列
的两根.数列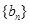 的前
的前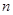 项和为
项和为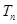 ,满足
,满足
(Ⅰ)求数列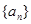 ,
,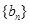 的通项公式;
的通项公式;
(Ⅱ)设数列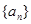 的前
的前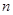 项和为
项和为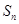 ,记
,记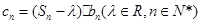 .若
.若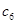 为数列
为数列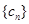 中的最大项,求实数
中的最大项,求实数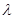 的取值范围.
的取值范围.
某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为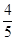 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为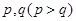 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
 |
(Ⅰ)求该公司至少有一种产品受欢迎的概率;
(Ⅱ)求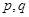 的值;
的值;
(Ⅲ)求数学期望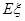 .
.
如图,四棱锥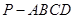 的底面
的底面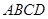 是矩形,
是矩形,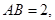
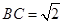 ,且侧面
,且侧面 是正三角形,平面
是正三角形,平面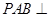 平面
平面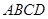 ,
,
(Ⅰ)求证: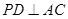 ;
;
(Ⅱ)在棱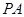 上是否存在一点
上是否存在一点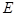 ,使得二面角
,使得二面角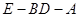 的大小为45°.若存在,试求
的大小为45°.若存在,试求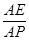 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.