已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
已知从“神州”飞船带回的某种植物种子每粒成功发芽的概率都为 ,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
,某植物研究所进行该种子的发芽实验,每次实验种一粒种子,每次实验结果相互独立,假定某次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败.若该研究所共进行四次实验,设ξ表示四次实验结束时实验成功的次数与失败的次数之差的绝对值.
(1)求随机变量ξ的数学期望E(ξ);
(2)记“函数f(x)= x2- x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
x-1在区间(2,3)上有且只有一个零点”为事件A,求事件A发生的概率P(A).
选修4-5:不等式选讲(本小题满分10分)
设函数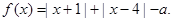
(1)当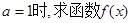 的最小值;
的最小值;
(2)若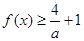 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数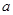 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程(本小题满分10分)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.曲线C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为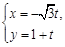 (t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
选修4-2:矩阵与变换(本小题满分10分)
已知矩阵A=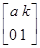 (k≠0)的一个特征向量为α=
(k≠0)的一个特征向量为α=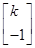 ,
,
A的逆矩阵A-1对应的变换将点(3,1)变为点(1,1).求实数a,k的值.
选修4-1:几何证明选讲(本小题满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.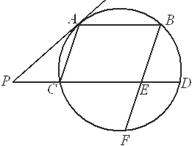
(1)求AC的长;
(2)求证:BE = EF.