如图，一次函数y=3x的图象与反比例函数
的图象的一个交点为A(1,m)．
（1）求反比例函数
的解析式；
（2）若点P在直线OA上，且满足PA=2OA，直接写出点
的坐标(不写求解过程)．
已知∠1=∠2，∠D=∠C求证：∠A=∠F
如图是甲、乙两人同一地点出发后，路程随时间变化的图象．
（1）此变化过程中，__________是自变量，_________是因变量．
（2）甲的速度是 ________千米/时，乙的速度是________千米/时
（3）6时表示_________________________
（4）路程为150千米，甲行驶了____小时，乙行驶了_____小时．
（5）9时甲在乙的________（前面、后面、相同位置）
（6）分别写出甲乙两人行驶的路程s（千米）与行驶的时间t(小时)的函数关系式(不要求写出自变量的取值范围)
S甲=___________________________
S乙=_____________________________
作图题：
如图，一块大的三角板ABC，D是AB上一点，现要求过点D割出一块小的角板ADE，使∠ADE=∠ABC，请用尺规作出∠ADE．(不写作法，保留作图痕迹，要写结论)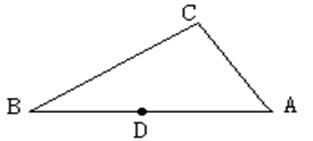
利用乘法公式简算（每小题4分，共16分）
（1）1102－109×111
（2）98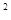
（3）(x+3y+2)(x—3y+2)
（4）化简求值：
，其中
，
计算题（每小题3分，共12分）
（1）
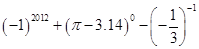
（2）(2a＋b)4÷(2a＋b)2
（3）
（4）（15x4y2－12x2y3－3x2）÷(－3x2)