如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半⊙O’与y轴正半轴交于点C,连接BC,AC.CD是半⊙O’的切线,AD⊥CD于点D.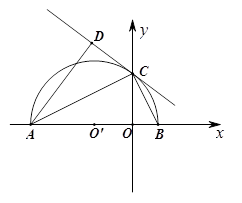
(1)求证:∠CAD =∠CAB;
(2)已知抛物线 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
.
① 求抛物线的解析式;
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
(·湖北孝感) 如图,一条公路的转弯处是一段圆弧(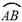 ).
).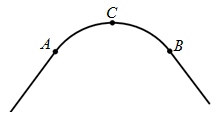
(1)用直尺和圆规作出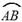 所在圆的圆心
所在圆的圆心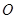 ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若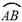 的中点
的中点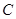 到弦
到弦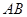 的距离为
的距离为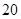 m,
m,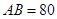 m,求
m,求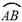 所在圆的半径.
所在圆的半径.
(·湖北襄阳,25题)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.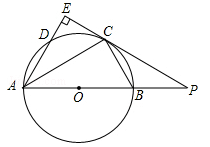
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
(·湖北武汉,21题,分)(本题8分)如图,AB是⊙O的直径,∠ABT=45°,AT=AB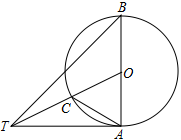
(1)求证:AT是⊙O的切线
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC的值
(·湖北荆门,22题,分)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证: ;
;
(3)若⊙O的半径为5,sinA= ,求BH的长.
,求BH的长.
(·湖北黄冈,21题,分)已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O 交AB 于点M,交BC 于点N,连接AN,过点C 的切线交AB 的延长线于点P.
(1)求证:∠BCP=∠BAN;
(2)求证: .
.