如图在平面直角坐标系内,以点C(1,1)为圆心,2为半径作圆,交x轴于A、B两点,开口向下的抛物线经过A、B两点,且其顶点P在⊙C上。
(1)写出A、B两点的坐标;
(2)确定此抛物线的解析式;
(年甘肃白银、定西、平凉、酒泉、临夏10分)如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.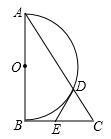
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
(年福建厦门10分)已知A,B,C,D是⊙O上的四个点.
(1)如图甲,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图乙,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
(年广西南宁10分)如图甲,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A,E,F三点作圆,如图乙. 若EC=4,∠CEF=15°,求 的长.
的长.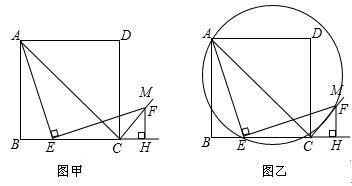
(年广西北海10分)如图(1),E是正方形ABCD的边BC上的一个点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE;过点F作FG⊥BC交BC的延长线于点G.
(1)求证:FG=BE;
(2)连接CF,如图(2),求证:CF平分∠DCG;
(3)当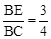 时,求sin∠CFE的值.
时,求sin∠CFE的值.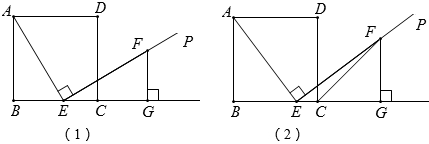
(年广西百色10分)如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.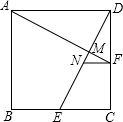
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2AD•NF=DE•DM.