如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．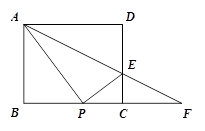
（1）当点P在线段BC上时（点P与点B，C都不重合），试用含a的代数式表示CE；
（2）当a=3时，连结DF，试判断四边形APFD的形状，并说明理由；
（3）当tan∠PAE=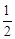
时，求a的值．
如图，△ABC是⊙O的内接三角形，AB为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE．
（1）求证：CE是⊙O的切线；
（2）若AC＝4，BC＝2，求BD和CE的长．
某种商品的标价为400元/件，经过两次降价后的价格为324元/件，并且两次降价的百分率相同．
（1）求该种商品每次降价的百分率；
（2）若该种商品进价为300元/件，两次降价共售出此种商品100件，为使两次降价销售的总利润不少于3120元．问第一次降价后至少要售出该种商品多少件？
如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．
（1）求证： ；
（2）连接BF，若 ， ， 求平行四边形ABCD的面积．
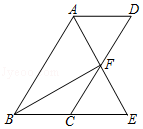
二孩政策的落实引起了全社会的关注，某校学生数学兴趣小组为了了解本校同学对父母生育二孩的态度，在学校抽取了部分同学对父母生育二孩所持的态度进行了问卷调查，调查分别为非常赞同、赞同、无所谓、不赞同等四种态度，现将调查统计结果制成了如图两幅统计图，请结合两幅统计图，回答下列问题：
（1）在这次问卷调查中一共抽取了 名学生，a＝ %；
（2）请补全条形统计图；
（3）持“不赞同”态度的学生人数的百分比所占扇形的圆心角为 度；
（4）若该校有3000名学生，请你估计该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和．
计算：