某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3120元.问第一次降价后至少要售出该种商品多少件?
如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上)
①把 沿 方向平移,请在网格中画出当点 移动到点 时的△ ;
②把△ 绕点 按逆时针方向旋转 后得到△ ,如果网格中小正方形的边长为1,求点 旋转到 的路径长.

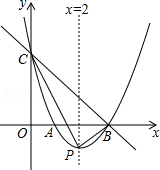
如图,直线 与 轴、 轴分别相交于点 、 ,经过 、 两点的抛物线 与 轴的另一个交点为 ,顶点为 ,且对称轴为直线 .
(1)求该抛物线的解析式;
(2)连接 、 ,求 的面积;
(3)连接 ,在 轴上是否存在一点 ,使得以点 , , 为顶点的三角形与 相似?若存在,求出点 的坐标;若不存在,请说明理由.
凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优惠方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价 (元 ,因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售 只时,所获利润 (元 与 (只 之间的函数关系式,并写出自变量 的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当 时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
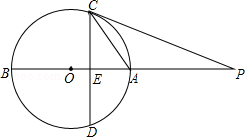
如图, 是 的直径,点 在 的延长线上,弦 ,垂足为 ,且 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.
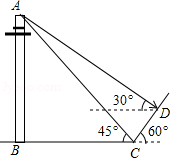
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线 恰好落在水平地面和斜坡上,在 处测得电线杆顶端 的仰角为 ,在 处测得电线杆顶端 得仰角为 ,斜坡与地面成 角, ,请你根据这些数据求电线杆的高 .
(结果精确到 ,参考数据: ,