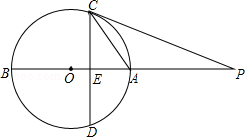
如图, 是 的直径,点 在 的延长线上,弦 ,垂足为 ,且 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.
如图,一次函数y=kx+b的图象与反比例函数y=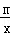 的图象相交于点A(﹣1,2)、点B(﹣4,n)
的图象相交于点A(﹣1,2)、点B(﹣4,n)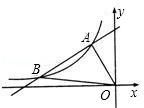
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
已知双曲线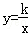 与直线
与直线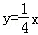 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线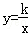 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,﹣n)作NC∥x轴交双曲线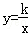 于点E,交BD于点C.
于点E,交BD于点C.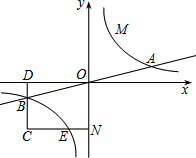
(1)若点D坐标是(﹣8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
已知,如图,正比例函数y=ax的图象与反比例函数y=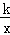 的图象交于点A(3,2)
的图象交于点A(3,2)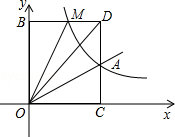
(1)填空:a= ;k= .
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
①当BM=DM时,求△ODM的面积;
②当BM=2DM时,求出直线MA的解析式.
如图,双曲线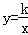 (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
如图所示,在直角坐标系xOy中,一次函数y1=k1x+b(k≠0)的图象与反比例函数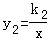 (x>0)的图象交于A(1,4),B(3,m)两点.
(x>0)的图象交于A(1,4),B(3,m)两点.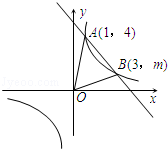
(1)试确定上述反比例函数和一次函数的表达式;
(2)在第一象限内,x取何值时,一次函数的函数值大于反比例函数的函数值;
(3)求△AOB的面积.