已知函数f(x)＝ex－ln(x＋m)．
(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；
(2)当m≤2时，证明f(x)>0.
设二次函数
，对任意实数
，有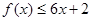
恒成立；数列
满足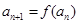
.
（1）求函数
的解析式和值域；
（2）证明：当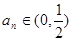
时，数列在该区间上是递增数列；
（3）已知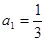
，是否存在非零整数
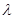，使得对任意
，都有
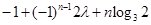恒成立，若存在，求之；若不存在，说明理由.
已知函数
为奇函数.
（1）求常数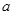
的值；
（2）判断函数的单调性，并说明理由；
（3）函数
的图象由函数
的图象先向右平移2个单位，再向上平移2个单位得到，写出的一个对称中心，若
，求
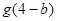的值.
上海某化学试剂厂以x千克/小时的速度生产某种产品（生产条件要求
），为了保证产品的质量，需要一边生产一边运输，这样按照目前的市场价格，每小时可获得利润是
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元，求x的取值范围；
(2)要使生产运输900千克该产品获得的利润最大，问：该工厂应该选取何种生产速度？并求最大利润.
在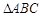
中,已知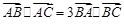
.
(1)求证: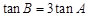
;
（2）若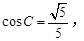
求角A的大小.
如图，正三棱柱ABC—A1B1C1的各棱长都相等，M、E分别是
和AB1的中点，点F在BC上且满足BF∶FC=1∶3.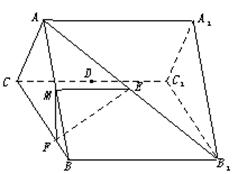
(1)求证：BB1∥平面EFM；
(2)求四面体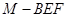
的体积.